Abstract:
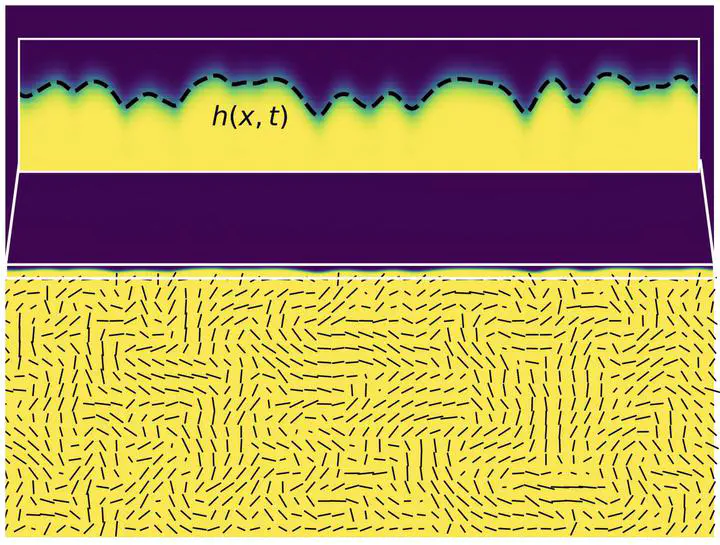
Active liquid crystals exert nonequilibrium stresses on their surroundings through constant consumption of energy, giving rise to dynamical steady states not present in equilibrium. The paradigmatic example of an active liquid crystal is a suspension of microtubule bundles powered by kinesin motor proteins, which exhibits self-sustained spatiotemporal chaotic flows. This system has been modelled using continuum theories that couple the microtubule orientation to active flows. Recently the focus has shifted to the interfacial properties of mixtures of active liquid crystals and passive fluids. Active/passive interfaces have been shown to support propagating capillary waves in the absence of inertia and offer a promising route for relating experimental parameters to those of the continuum theory. In this paper we report the derivation of a minimal model that captures the linear dynamics of the interface between an active liquid crystal and a passive fluid. We show that the dynamics of the interface, although powered by active flows throughout the bulk, is qualitatively captured by equations that couple non-reciprocally interface height and nematic director at the interface. This minimal model reproduces the dynamical structure factor evaluated from numerical simulations and the qualitative form of the wave dispersion relation seen in experiments.